ARC099に参加した(210位) - 天色グラフィティ

f:id:ejinote:20180624151041p:plain

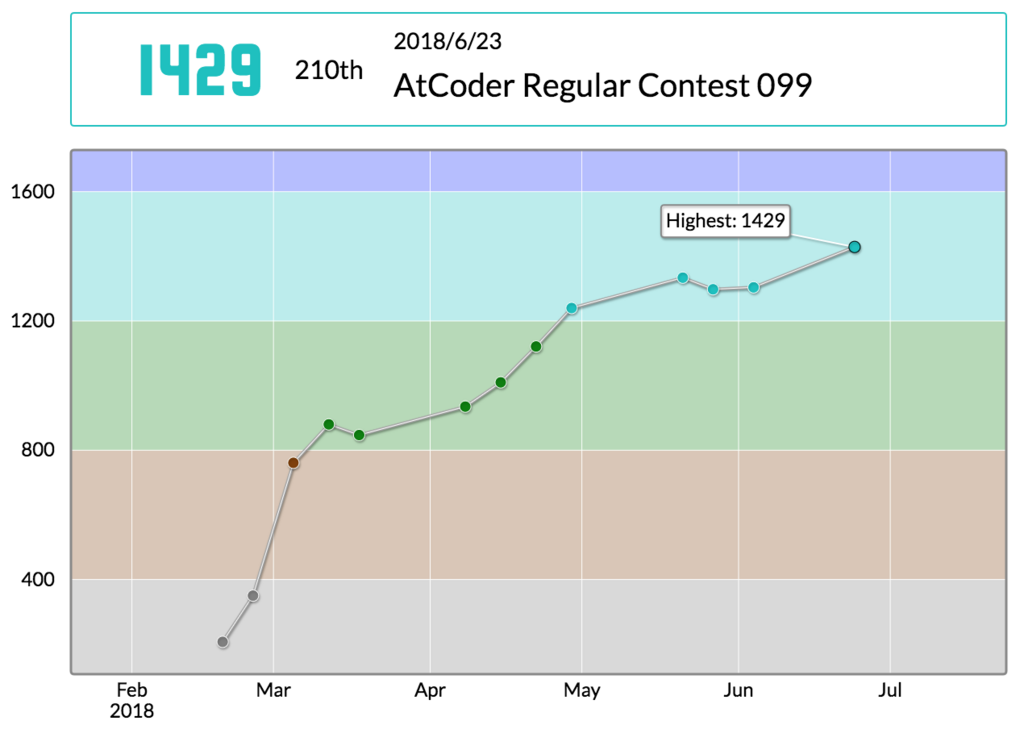
ARC099に参加しました。210位でレートは1304→1429になりました。久しぶりのコンテスト参加で緊張しましたが、Dをそれなりに早く解いたのがよかったっぽいです。

そういえば先日書いた記事がホッテントリに載りました。結構うれしいものですね。

amalog.hateblo.jp

振り返り

C - Minimization

最小値が1なので、全要素を1にすればよい
1回適用すると1がK-1個増える

1を中心に左右に1を広げていくイメージで解きました。1の左右それぞれについて端から最適な回数で処理をして、1の周りの余りはよしなにやる感じ。

import math
n, k = map(int, input().split())
A = list(map(int ,input().split()))
print(math.ceil((n-k)/(k-1)+1))

D - Snuke Numbers

手で書いても全く分からなかったので実験しました。

import matplotlib.pyplot as plt
%matplotlib inline

def digit_sum(i):
    return sum(map(int, list(str(i))))

scores = [i/digit_sum(i) for i in range(1, 50000)]
plt.figure(figsize=(10, 5))
plt.scatter(list(range(1, 50000)), scores, s=1)
plt.show()

f:id:ejinote:20180625171837p:plain

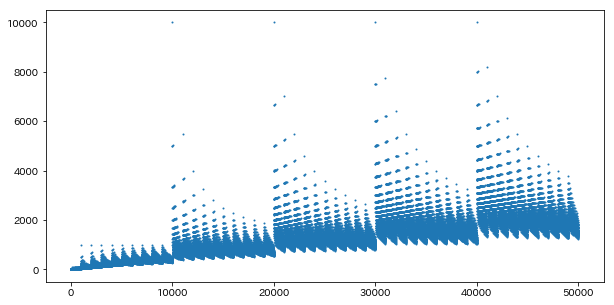
規則性があることがわかります。ちなみにスコアがジャンプするのは繰り上がりが起きるときなので、XXX999みたいな数にだけ着目すればよいと分かります。

XXX999みたいな数それぞれについて、次のやつとの比較を行って、だめだったら消せば良いと思います。

実装は鬼汚いです。

def digit_sum(i):
    return sum(map(int, list(str(i))))

def score(head, tail):
    return num(head, tail)/digit_sum(num(head, tail))

def num(head, tail):
    return int(str(head)+tail)

k = int(input())
tail = ''
head = 0
cnt = 0
last = 0
while True:
    head += 1
    if score(head, tail) <= score(head+1, tail):
        if num(head, tail) > last:
            print(str(head)+tail)
            last = num(head, tail)
            cnt += 1
            if cnt == k:
                break
    else:
        head = 0
        tail += '9'