ARC100に参加した(510位)

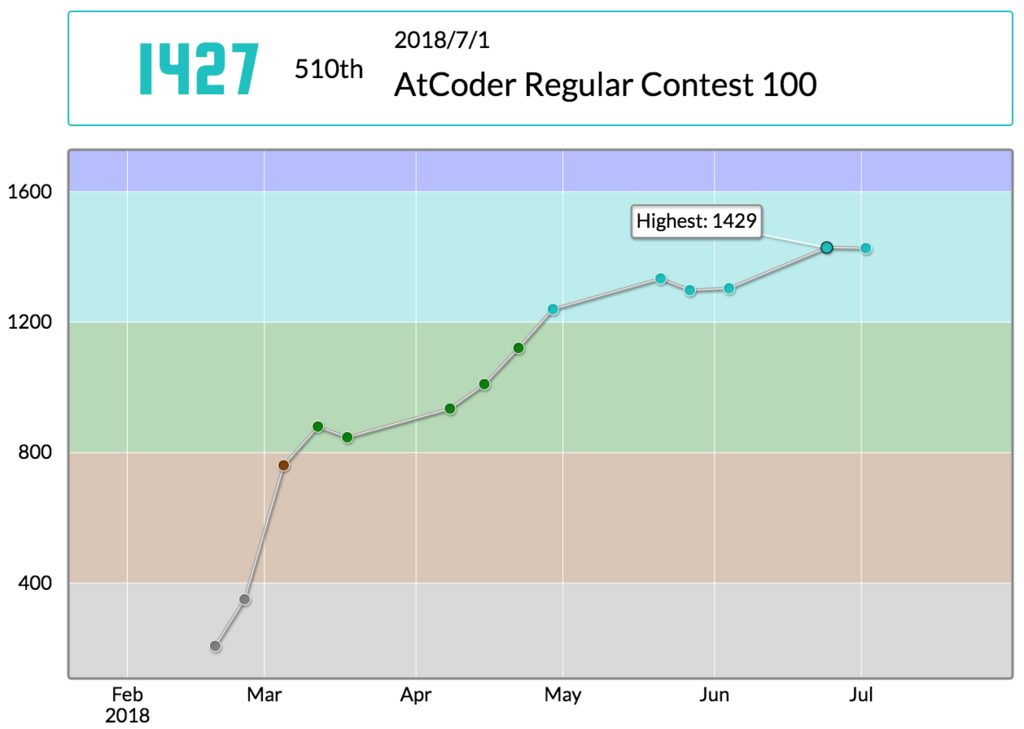
ARC100に参加しました。結果は510位で、レートは1429→1427と微減しました。

問題としてはC問題を1WAしながらACし、D問題が解けませんでした。久しぶりにDで手こずった気がします。

今回から、解けなかった問題については典型要素の抽出をやってみたいと思います。

前回の記事：

amalog.hateblo.jp

振り返り

C - Linear Approximation

数列と整数についての最小値を求める問題。

予め数列からを引いておけば、あとはL1ノルムを最小化する代表値(=中央値)をに設定すればよい。

思いつくためには、横軸、縦軸のプロットを書いてみるとよい。横線を一本引いたときに、その横線より上に来てる点と下に来てる点が同じ数のところが最善であることに気がつくはず。

#!/usr/bin/env python
N = int(input())
A = list(map(int, input().split()))
A = sorted([a-(i+1) for i, a in enumerate(A)])
m = A[N//2]
ans = 0
for a in A:
    ans += abs(a-m)
print(ans)

D - Equal Cut

数列を4つに分けて、それぞれの和の最大と最小の差を最小化する問題。

端から貪欲でやるのはNG。たとえば1, 1, 1, 1, 10000とかのとき、1つの部分の合計は理想的には合計/4=2501だけど、2501になるように貪欲でとっていくと4つに分けられない。

解法は以下の通り。

1. まず2つに分け終わったとする
2. それぞれの部分については、理想的な分割箇所(=2つの合計ができるだけ近くなるとこ)は一意に定まる
3. なので、最初の分割点を全探索して、それぞれの部分は理想的な分割にすれば、トータルの理想的な分割も定まるはず
4. ちなみに、最初の分割点を右にずらすと、2段階目の分割点はそれぞれ変わらないor右にずれるのいずれかになるので、探索を減らせる

こんな感じ。これはできてもよかったな……

典型要素としては、

• 区間の累積和は予め全体の累積和を取っておけば差を利用することでで求まる
• 「ここさえ探索すればあとは一意に定まる」みたいな感じで探索すべき場合の数を減らす

ってなところか。

#!/usr/bin/env python
from itertools import accumulate

N = int(input())
A = list(map(int, input().split()))
Acum = list(accumulate([0] + A))

def cumsum(left, right):
    # [i, j)
    return Acum[right] - Acum[left]

def find_best_cut(left, right, prev):
    prev = max(prev, left+1)
    now = prev
    res = now
    best = abs(cumsum(left, prev) - cumsum(prev, right))
    while True:
        now += 1
        score = abs(cumsum(left, now) - cumsum(now, right))
        if score < best:
            best = score
            res = now
        else:
            return res

left = 0
right = 0
best = float('inf')
for center in range(1, N-1):
    left = find_best_cut(0, center, left)
    right = find_best_cut(center, N, right)
        
    t = [cumsum(0, left), cumsum(left, center), cumsum(center, right), cumsum(right, N)]
    score = max(t) - min(t)
    if score < best:
        best = score
    
print(best)

気づいたこと

D問題まではPythonで書いて、E以降はC++で書こうと思っていたけど、E問題が解ける頻度はまだ少ないからC++で書く練習がなかなか積めないという問題点に気づいた。