2022年を読んだ本とともにふりかえる

2022年もおつかれさまでした。今年は3月に転職を行い、業務内容もデータサイエンスよりエンジニアリング(MLOps)に近い領域に変わりました。来年はさらに変わりそうな気配がしています笑。
というわけで読んだ本をざっくり紹介しつつ、2022年を振り返っていければと思います。
機械学習・データサイエンス関連
エンジニアリングに軸足を移したとはいえ、あまり機械学習関連の本を読めていませんね……?
データサイエンス系VTuberアイシア=ソリッドの中の人が書いた本。表紙だけ見ると初心者向けで薄く広く書いてあると思われるかもしれませんが、回帰分析やロジスティック回帰から始めて、深層学習や強化学習など実践的な範囲を、必要十分な深さでじっくり解説してくれる本です。
データ基盤に興味が湧いたらまっさきに読むべき本。データ基盤とはなにかという基礎的な部分から、実際に作るにあたっての泥臭い(人間が絡む)部分まで解説されています。
DevOps関係
転職してからMLOps的な仕事をすることも多かったので近接領域であるDevOps関係の本を読みました。
DevOpsをやるにあたってGoogle Cloudの機能で避けてきた領域(=ネットワークとかセキュリティとか)があったために購入。隅々まで読んだわけではないですが、クラウド関係で困ったことがあったときに索引からたどって読むようにしています。
チームのありかたやドキュメンテーション、テストなどDevOps以外のプラクティスが詰め込まれている本。「いやそれGoogle規模でしかムリやろ」と思う記述もちらほらありますが、学べるものは多いはず。チームで輪読会などをするのも良いと思います。
開発にあたって正しいと思っていたことを修正してくれる本。たとえば「本番デプロイは危ないんで専門チームがやりますね!」とかがアンチパターンであることが分かります。
ハイパフォーマンスを出すための文化と仕組みについて触れている本。DevOpsやアジャイルと言われると開発の技法と思われがちだが、それがビジネスとしてもインパクトがあることを解説している(と理解しました)。事例も書かれているのでもう一度読み返そうと思っています。
システムの監視とその改善方法について解説している本。システムの運用に触れ始めたらざっと読んでおくと良いと思います。あとは実際に作ったシステムが関係する部分を都度参照する感じ。
スクラム関係
9月からはチームでスクラムマスター的な動きをしていました。読んだ本は以下の4冊+最新版のスクラムガイド。
3ヶ月やってみた一番の学びは「教科書どおりやってみることの重要性」です。スクラムイベントを省いたり短縮したりすることなく、最初は教科書どおりやってみて、スプリントを回すたびに少しずつチームで変えていくというプロセスが大事です。
まずこれを読みましょう。ストーリー形式でスクラムのやりかたをなぞってくれると同時に、やってしまいがちなミスも紹介してくれるのでチームの目線を合わせるのによい本だと思います。
ふりかえり=KPTと思っている人はいませんか? この本にはシチュエーションに合わせておすすめのふりかえり手法を紹介してくれているため、ふりかえりのファシリテーターになったらこの本を手元に置いておくと良いです。
スクラムマスターの仕事だけではなく、どのような態度で臨むか、どのようなことを考えるべきかなどメンタリティの部分に言及している本です。上の2冊を読んでスクラムをやってみて、もっとスクラムマスターとして成長したいと思ったときに読むのが良さそうです。
こちらもストーリー形式でチームが良くなっていく様子を解説してくれる本です。読み物として。
その他
めちゃ有名な本なので読んでいる人も多いはず。「不確実性」というキーワードを切り口にして組織で起こる出来事を解説している本。人によって刺さる章が違う気がするのでぜひ読んで見てほしいし、周りのエンジニアでない人にも勧めてほしいです。
現職にEM(=エンジニアリングマネージャー)っていうポジションがあり、前職にはなかったのでいったいどんな仕事なんやって思って読んだ本。「ふーんそういうものなのか」っていう浅い感想に終わってしまったのでしばらく寝かせてもうちょっと理解できるタイミングを待とうと思います。
漫画
主にKindleでいろいろ読んだので特におすすめなものを3シリーズ。
おわりに
2022年も大変お世話になりました。仕事でも新しい領域にチャレンジするようになり、なかなか落ち着いてブログを書く時間と心の余裕が取れないですが、来年こそは少しずつ再開できればと思っています。(ひさしぶりにブログ書こうと思ったら全然手が動かなくて愕然としました)
2023年もよろしくお願いします。
ワンフレーズで本と出会うサービス「一文一会」を作りました
ここ2週間くらい力を入れて開発していた「一文一会」というサービスが完成しました。
本のフレーズや紹介文がつぎつぎ(ランダムに)表示されるサービスです。

ビビッときたフレーズをクリックすると何の本なのか知ることができます。

好きな本を紹介することもできます。

もしよろしければ先にサービスを触ってみてください(そしてできれば新しいフレーズの登録もお願いします)
なぜ作ったのか
いまの世の中にはレコメンドが溢れています。どんなアプリを触っていても「おすすめ」という形で自分の好みにあったコンテンツが提示されつづけます。 好みのコンテンツが出ること自体は望ましいですが、セレンディピティ(素敵な偶然に出会うこと)を感じる機会は減ってしまっています。
たとえば、本屋をぶらぶら歩いてポップを眺めて、いままで読んだことがないようなジャンルの本を買うとか。
そんな体験をネット上で作れないかと考え、このサービスを思いつきました。
(実はこのアイディア自体は以前Railsで実現したことがあるのですが、その時からは技術力が上がったのでリメイクすることにしました)
どう作ったのか
ざざっと使った技術・サービスについて書きます。
- React
- Next.js
- tailwindcss
- firebase + firestore
- react-spring
- cloudinary
React + Next.js
フロントエンドフレームワークはReactとNext.jsを採用しました。Among Us Noteのときも採用した技術スタックです。
ウェブサイトのパーツをコンポーネントという形で適切なサイズに切り分けておけば、以前書いたコードを使い回すこともできて幸せです。
デプロイは以前と同様Vercelにしています。個人開発なら無料で使えます。
tailwindcss
巷で流行っていると噂のCSSフレームワークです。見た目を作るのに使いました。
他のCSSフレームワークは「ボタン」「ナビバー」「フッター」のような単位でCSSクラスが定義されているのに対し、tailwindcssは p-3 text-gray-700 、h-screen などのCSSクラスを複数組み合わせて見た目を作っていきます。
生のCSSを書く代わりにCSSクラスをぺたぺた切り貼りしていくイメージです。
最初はボタンひとつ作るのにも苦労するので、tailwindcssを採用するメリットは分かりづらいかもしれませんが、tailwindcssの良さは細かい見た目の調節が必要になったころから感じられるようになります。
Firebase + Firestore
FirebaseはBaaS(Backend as a Service)のひとつです。バックエンドとして良く使われるデータベースや認証などの機能をまるっと提供しています。 Firebaseを採用すればバックエンドの実装をほとんど行わなくて済むため、フロントエンド(特にユーザー体験)の開発に集中することができます。個人開発の味方……
今回はFirebaseの中でもFirestoreというデータベースを利用しています。
react-spring
ふわっとフレーズが現れて消えるアニメーションの実装に使いました。
react-springの useTransition を使うことで、DOMが追加されたとき、更新されたとき、消されたときにアニメーションを付与することができます。
↓ 公式のデモです
Cloudinary
OGPの生成のために使いました。Cloudinaryは画像や動画などのマルチメディア管理サービスです。Cloudinaryに画像をアップロードした後、その画像をクロップしたり、テキストを重ねたりして配信することができます。 なかなか大きな無料枠があるので、個人開発でも十分使えるのではないかと思っています。
↓ こんな感じでテンプレートをアップロードしておきます

↓ のようなURLにアクセスすることで画像に文字を重ねることができます
https://res.cloudinary.com/dv2ewdcmt/image/upload/l_text:[fontFamily]_[fontSize]:[text],w_[width],c_fit/vxxxxxxxx/filename.jpg

Google Fontsにある日本語フォントを使えるそうなのですが、現状すべての日本語フォントが使えるというわけではないです(2021年3月12日現在)。 そこでGoogle Fontsからフォントファイルをダウンロードして、Cloudinaryにアップロードするという方法を使いました。
具体的な方法は↓の記事のコメント欄をご覧ください。 qiita.com
(最初は vercel/og-image を使っていましたが、日本語フォントを使おうと思うと無料枠ではレスポンスが遅く、使い物になりませんでした)
まとめ
React + Next.js + tailwindcssで本と出会えるサービスを作りました。
バックエンドはFirebaseに丸投げすることで手間をガツッと削減しました。
無事リリースもでき、ブログも書き終わったのでオグリキャップを育てたいと思います。オグリキャップしか勝たん。
参考文献
【discord.py】Among Usのためにランダムに人を選ぶDiscord Botを作りました
現在このbotは公開を停止しています。申し訳ありません。

discord.pyを使ってDiscordのbotを2時間くらいで作った話を書きます。
なんで作ったか
Among Usはクルーメイト(村人)とインポスター(人狼)が争うゲームなのですが、MODを利用して「狂人」「てるてる」などの新役職を入れることができます。
ただし、MODを利用できるのはsteam経由だけなので、iOSやSwitchから参加している人は利用することができません。
そこで、ゲーム内の機能として利用するのではなく、DiscordのDMで通知を送ることでゲーム外で新役職を利用しようと考えました。
仕様
Botの仕様
- Discordのコマンドとして
.dartsコマンドを実装する .darts [channel_name]でchannel_name(ボイスチャット)に入っているメンバーからランダムに1人選ぶ- 選ばれた人にDMを送る
デプロイ
実装
Botの用意
Discord Developer PortalからApplicationを作成します。
詳しくはこちらの記事が参考になります(感謝!)
discord.pyでの実装
discord.pyを使います。
discord.Client を使うパターンと、discord.ext.commands を使うパターンがあります。
今回のように引数を取るコマンドの場合、discord.ext.commands を使うのが扱いやすいです。
@bot.command() デコレータをつけることで、その関数をコマンドとして扱うことができます。
第1引数は commands.Context が入ってきており、コマンドが叩かれたチャンネルやその文章などの内容が含まれています。
第2引数以降を定義した場合、そのままコマンドの引数になります。
@bot.command() async def darts(ctx: commands.Context, channel_name: str): if ctx.author.bot: return await ctx.message.delete() channel_name = channel_name.lstrip("#") channels = ctx.guild.voice_channels # ボイスチャンネルリストを取得 for ch in channels: if ch.name == channel_name: if not ch.members: await ctx.send(f"#{channel_name}には誰もいません") return member = random.choice(ch.members) await member.send("あなたが選ばれました!") return await ctx.send(f"#{channel_name}が存在しません")
ハマったポイント
ボイスチャットに入っているメンバーを取得するには、Bot側とスクリプト側の両方に設定が必要でした。
Bot側
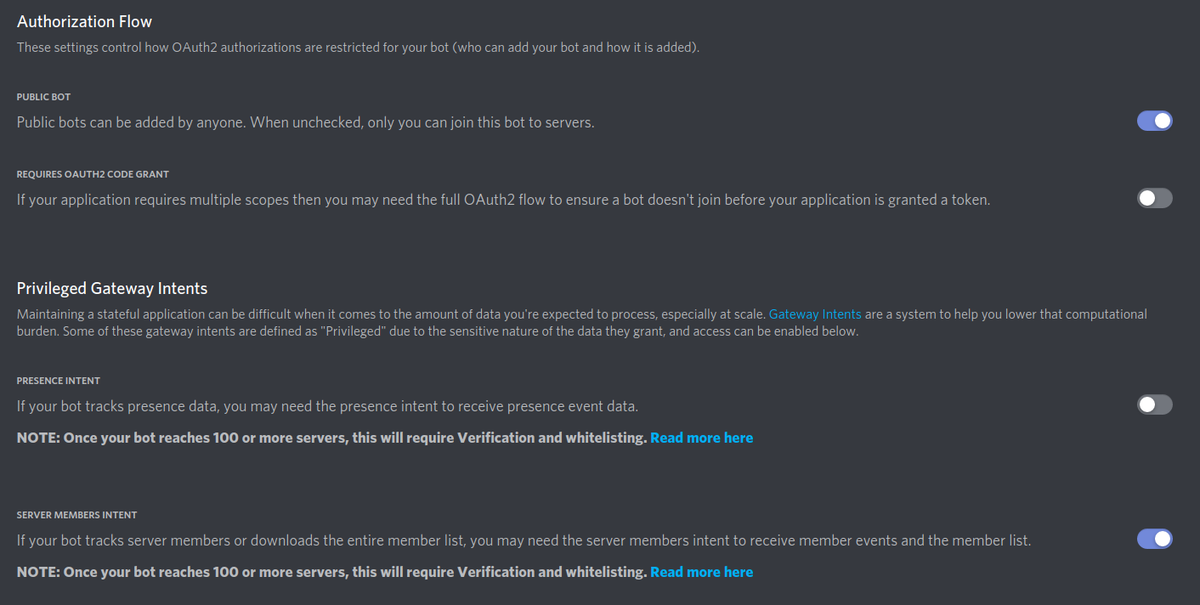
botの設定ページから SERVER MEMBERS INTENT をオンにします。
スクリプト側
import discord from discord.ext import commands intents = discord.Intents.default() intents.members = True bot = commands.Bot(command_prefix=".", intents=intents)
コード全体
import os import random import discord from discord.ext import commands from typing import Optional intents = discord.Intents.default() intents.members = True bot = commands.Bot(command_prefix=".", intents=intents) @bot.command() async def darts(ctx: commands.Context, channel_name: str, name: Optional[str] = None): if ctx.author.bot: return await ctx.message.delete() channel_name = channel_name.lstrip("#") channels = ctx.guild.voice_channels for ch in channels: if ch.name == channel_name: if not ch.members: await ctx.send(f"#{channel_name}には誰もいません") return member = random.choice(ch.members) msg = f"{name}に選ばれました!" if name is not None else "あなたが選ばれました!" await member.send(msg) return await ctx.send(f"#{channel_name}が存在しません") TOKEN = os.environ.get("DISCORD_BOT_TOKEN") bot.run(TOKEN)
まとめ
discord.pyは手軽に使えて便利。slack関係のライブラリも見習ってほしい
ソースコードはこちらです
参考文献
【Next.js】Among Usが好きすぎて3日間でAmong Us用メモアプリを作りました【個人開発】
こんにちは。鈴木天音(@SakuEji)です。
今日はこの間作ったAmong Us NoteというAmong Us用メモアプリについて書きます。
Among Usが好きすぎて、Among Usのメモを手軽に取れるWebアプリを作りました🎉🎉🎉
— 鈴木天音|Amane Suzuki (@SakuEji) 2021年2月19日
・遊びながらでもぽちぽち簡単メモ
・信用できる人と怪しい人をターンごとに整理
・議論のおともにどうぞ
拡散していただけると嬉しいです!#AmongUsNote https://t.co/AMIa4wTfzD
こんな感じ↓の雰囲気で、各ターンごとに怪しい人/信じられる人をぽちぽちメモする感じです。

PC上でAmong Usの画面に並べて使ってもいいですし、スマホでメモを表示しておいてもいいです。 どちらでもうまく表示されるようにレスポンシブで設計しています。良かったら使ってみてください!
このサービスを作った理由
最近知り合いのKagglerたちとわいわいAmong Usをやっています。 そのときに手軽でシンプルなメモアプリが欲しい場面(初日怪しかった人を忘れちゃうとか、自分自身の白要素を忘れてうまく弁明できないとか)があったので作りました。
使っている技術・サービス
使っている技術やサービスをざっとリストに書き出すとこんな感じです。
- 機能本体
- React
- Next.js
- 見た目
- Bulma (react-bulma-components)
- styled-components
- fontawesome
- figma
- ホスティング
- Vercel
- 開発まわり
- eslint
- prettier
- husky
- GitHub project
- その他
以下では主要なものについて紹介します。
Next.js
ReactをベースにSSR(サーバーサイドレンダリング)などの機能を足して使いやすくしたフレームワークです。
僕はフロントエンド初心者なのですが、 Reactを単独で使うよりNext.js経由で使うほうが(初動の学習コストは高くなるものの)コードを簡潔に保ちやすい印象です。
Typescriptは厳密さと書きやすさのバランスがちょうどよくて結構好きです。
Next.jsを使ってWebアプリを作った場合、Vercelでホスティングするのが断然おすすめ。 GitHubのリポジトリを指定すれば自動でビルドしてデプロイしてくれます。独自ドメイン対応も簡単。 masterブランチをproduction環境に、developブランチをdevelop環境にといった出し分けもやってくれるので、 Next.jsはVercel前提のフレームワークだと考えたほうがいろいろ幸せです。 個人開発だと無料で使えます。
Vercelに出会う前はFirebase hostingとFirebase functionsを併用してがちゃがちゃやっていましたが、もう面倒なことをせずにすみますね。
Bulma
シンプルできれいなCSSフレームワークです。 見た目をちゃちゃっと組み上げるのに使っています。
BootstrapやMaterial UIあたりと選択になるのかと思いますが、Bulmaはいちばんかわいくて親しみやすい雰囲気を出すことができます。 逆に管理画面チックな雰囲気が良ければMaterial UIを使うと思います。
そのまま使おうとするとjQueryとReactを両方入れる必要があって気持ち悪いので、react-bulma-componentsを経由して使いました。
styled-components
プレイヤーの生死に応じて背景色を変えたりといった、細かい見た目の処理を行うために採用しました。
開発の進め方
個人開発は熱意が大事です。
特に僕は作っているものがエターナる(永遠に完成しない)傾向があるので、作りたい気持ちが続いている間にある程度形にすることを大事にしています。
作りたい気持ちを維持する方法はいくつかあって、
あたりがおすすめです。
今回はGitHub projectの作業可視化と、ドメイン取得を行いました。
GitHub projectの使い方
GitHub projectを使ってカンバン的な進捗管理を行いました。ツールはなんでも良いので、やるべきことを全部目の前に並べて、進んでいる感を出すことが大事です。

個人開発で「issue立てて、PR切って、あれこれ」みたいにやっているとスピード感が落ちてやる気を失ってしまうので、簡易版issueであるカードを活用します。
だいたいの手順は以下のとおりです。
- 作りたいものが思いつく
- GitHub Projectを作る
- ユーザーストーリーを書き出す
- 使うキャラクター色を選べる
- ターンごとにぽちぽちメモができる
- メモをリセットできる
- 死亡したプレイヤーがぱっと見でわかる
- くらいが最低限
- プロジェクトの遂行に必要なものを書き出す
- Next.jsのstarter projectを作る
- ドメインをとる
- OGP画像を作る
- など
- ユーザーストーリーを書いたカードに具体的なTODOを書き込む
- なにか調べ物をしたときは、対応するカードにリンクを書き込む
- あとで振り返ったり、別プロジェクトをするときに便利
あとは「In progress」にあるカードを常に1〜2枚に保ちながらすぱすぱカードを移動していくだけです。
今後追加したい機能
Twitterに「リリースしたよ」的な投稿をしたところ、何人かの方にフィードバックをいただきました。
その中でも優先度高めに対応したいものとして、
- 名前を記入できるようにする(色と対応付けて覚えるのが大変なので)
- ボタンの消費状況をメモできるようにする
というものがあります。この記事を書き終えたら実装を始める予定です。
振り返り
実際の作業時間が3日ほどで、かなりスピード感良く1st releaseをすることができました。
今回はNext.js+Bulma+Vercelという組み合わせで技術を採用しました。見た目やインフラ、CI/CDといった考え始めるとキリがない部分をよしなに吸収してくれるため 本質的な部分に集中しやすく、個人開発にかなり向いていると感じました。
自分で使ってみてまだまだ使いにくいところは残っているので、自分の中のAmong Usブームが過ぎ去らないうちに機能改善を進めていきたいです。
atmaCup #5に参加しました(Public2位→Private6位)

先週土曜日から今週土曜日にかけて1週間、atma社が主催するatmaCup #5に初参戦しました。
結果はPublic2位からのPrivate6位で、残念ながらメダルは逃す結果となりました( ´•̥ו̥` )クヤシイ
個人的には短期間のコンペで複数のモデルを試し、最終的にエレガントっぽい解法を作れたので満足しています。メダルほしかったけどね!!!
2020-06-07追記:実装を公開しました!
問題概要
- テーブルデータとスペクトルデータが与えられてとある現象が発生しているか否かを予測する2値分類問題
- 負例の多いimbalanced data
- 評価指標はPrecision-Recall CurveのAUC
- LightGBMもニューラルネットも同じくらいのスコアが出る(良問!)
解法
共通部分
- スペクトルにはscipyのSavitzky-Golay Filteringをかけた
- Savitzky-Golay Filteringをかける際にn次微分を算出し、それを新たなスペクトルとしてデータ拡張した
LightGBM
- テーブル部分は特に凝った特徴量作成はしていない
- スペクトル部分は、スペクトルをn次微分したものに対して集約をかけて特徴量を作成
- パラメータは温かみのある手動調節
- optunaのLightGBMTunerCVがコンペ中にリリースされ、意気揚々と試したが今回はworkしなかった
NN
- テーブル部分をMLPに通し、スペクトル部分をConv1Dに通し、concatして予測
- テーブル部分
- LightGBMのときに作った特徴をrankgaussにかけた
- スペクトル部分
- スペクトルの微分をチャネル方向に追加した
- 大きめのkernel_sizeが効いた
- 複数のkernel_sizeでConv1D→BatchNorm→ReLU→Dropout→GlobalMaxPoolしたものをconcatした
バリデーション
GroupKFoldとStratifiedKFoldを試した。CVとLBの動きに相関が取れていたStratifiedKFoldを採用した。
アンサンブル
OOFを見ながらLGBM:NN=0.25:0.75でrank averageした。爆死した。
コンペ中の動き
序盤(初日〜2日目)
微分が絶対に効くというのは最初から確信していたので、微分×ピーク周りの集約で特徴量を作り、LightGBMにかけた。
結果、早い段階でPublic 1位になり、スタートダッシュ完了。
やったね!#atmaCup pic.twitter.com/U5K3aB8f6U
— えじ|Amane Suzuki (@SakuEji) 2020年5月29日
しばらく同僚のtakuokoさんとshimacosくんとのデッドヒートを楽しむ。
中盤(3日目〜7日目)
平日で仕事があったためあまり時間を割けず、LightGBMの特徴量を機械的に作ろうと考えた。 tsfreshを利用して網羅的に特徴生成をしたあと、Null Importanceに基づいて特徴を削った。しかし、微分×ピーク特徴に全く勝てず、LB上の進捗はなし。
水曜日は有給をとって特徴量をちびちび手作りしていたが、これも効果なし。
悲しくなってオートチェスに逃げたが、オートチェスでも惨敗したので泣く泣くatmaCupに帰ってくる。
#atmaCup の息抜きにオートチェスやったら惨敗して悲しい気持ちになったのでatmaCupがんばります……
— えじ|Amane Suzuki (@SakuEji) 2020年5月30日
終盤(締切前日〜最終日)
DiscussionでNNが強いという噂を聞き、NNを作ろうと考える。
微分が効くのが分かっていたため、スペクトルの微分をチャネル方向に加え、Conv1Dに通すシンプルなモデルを作成。9位くらいに帰ってくる。
進捗した / Nice Hard Work ✒ 現在の順位は 9位です. https://t.co/eesc9F7U3q #atmaCup
— えじ|Amane Suzuki (@SakuEji) 2020年6月6日
kernel_sizeを大きくして、複数のkernel_sizeを並列すると良いことに気づき、5位に進捗。
よっしゃ / public LB は飾りです 現在の順位は 5位です. https://t.co/eesc9F7U3q #atmaCup
— えじ|Amane Suzuki (@SakuEji) 2020年6月6日
作っておいたLightGBMとアンサンブルして2位に。
1位が遠い / 勝ちたい! 現在の順位は 2位です. https://t.co/eesc9F7U3q #atmaCup
— えじ|Amane Suzuki (@SakuEji) 2020年6月6日
結果、shakedownして6位に。悲しみを背負う。NN single modelで出していたらprivate2位だった(なおこいつはCVはそんなに良くなかったので、たぶんどう頑張っても選べなかった)
public2位、private6位で残念ながらメダルはもらえませんでした><#atmaCup
— えじ|Amane Suzuki (@SakuEji) 2020年6月6日
感想
工夫のしがいがあるとてもよいコンペで、atmaCup初参戦ながらとても楽しめました。最近はあまりKaggleには触れていないのですが、データ分析コンペの感覚も少し取り戻すことができました。
面白い問題を用意し、コンペサイトのUIアップデートを含めて1週間コンペを盛り上げ続けてくださった運営の方々、本当にありがとうございました!
LBでいっしょにデッドヒートを繰り広げたみなさま、楽しかったです。入賞されたみなさま、おめでとうございます。次は負けないぞ〜〜〜
以上!
初めて技術書典に出展して、新刊を300部売るまで
9/22の技術書典7で『ハマって覚えるデータ分析・機械学習の罠』を頒布しました。
BOOTHでの同時販売を含めると、書籍とPDFで合計300部以上買っていただけました。 買ってくださった方々、ありがとうございました。 感想や改善点などはTwitterで@SakuEjiにメンションを飛ばしていただけたらとても嬉しいです。
技術書典行けなかったという人にはBOOTHでもPDF版を頒布しています。頒価は会場と同じく1000円です。
技術同人誌を書いたのは初めてでしたし、技術書典には参加者としてすら行ったことがなかったので不安9割でした。 そもそも完成できたのが奇跡としか言いようがありません。
売れ行きが全く想像できなかったのですが、「近頃話題の機械学習だし、なんとかなるやろ」とかなり強気に書籍は150部刷りました。 「売れ残ったらちょっと悲しいな」とも思っていましたが、 出だしからたくさんの方に買ってもらえて、14:00くらい(技術書典が11:00-17:00なので、だいたい半分の時間)に完売しました。
完売したことはすごく嬉しいのですが、「やっぱり書籍が欲しかった」という声も多くいただきました。 次回以降は気持ち多めに刷るくらいで良さそう、と思っています。 売れ残っても委託販売とかできますしね。
この記事では備忘録も兼ね、出展するに当たってやって良かったこと、やっておけば良かったことをまとめておきます。ぜひ参考にしてくださると幸いです。
何の本を出したか
『ハマって覚えるデータ分析・機械学習の罠』というタイトルからも分かる通り、データ分析や機械学習にまつわるアンチパターンをぎゅっと詰め込んだ本になっています。
機械学習初心者〜中級者が小規模な機械学習プロジェクト(研究とか、Kaggleを含む)に携わるという状況を想定しています。
機械学習プロジェクトを立ち上げるとき、データを眺めるとき、特徴量を作るとき、評価方法を決めるとき、学習するとき、と分析の各段階において気をつけるべき罠を一通り紹介した後、 分析サイクルを回すときに気をつけるべきことをTips的にまとめています。
会場に来てくださった方の中からも「あーこういうのあるよね」「これは知らなかった」という反応を多くいただき、嬉しい限りです。
より詳細な目次はこんな感じです。
はじめに 本書の想定している読者 あなたは誰ですか? 用語集 第1章 プロジェクトを始めるときの罠 1.1 機械学習が有効な分野を見誤っている 1.2 機械学習の結果をどう使うか想像できていない 詳しく知りたい方は 第2章 データを知るときの罠 2.1 データの背景を把握せずに解析を始めてしまう 2.2 データの統計量だけを見てしまう 2.3 可視化して満足してしまう 第3章 前処理・特徴量作成を行うときの罠 3.1 泥臭い作業から逃げてしまう 3.2 典型的な処理を知らない 3.3 特徴量作成にバグを埋め込んでしまう 3.4 リークを埋め込んでしまう 第4章 モデルを評価するときの罠 4.1 ベースラインを作成しない 4.2 評価指標をよく考えずに選んでいる 4.3 バリデーションを適切に行っていない 第5章 モデルを訓練するときの罠 5.1 モデルに適した形に前処理していない 5.2 ハイパーパラメータ探索を適当に行っている 第6章 分析サイクルを回すときの罠 6.1 ソースコードのバージョン管理を行っていない 6.2 ライブラリのバージョンを固定していない 6.3 乱数を適切に扱っていない 6.4 モデルを保存していない 6.5 Jupyter Notebook の収拾がつかなくなっている 6.6 パラメータをソースコード中に書き込んでいる 参考文献 おわりに
上の目次を読んで「あれ、これ良いかも?」と興味をもってくださった方はBOOTHからPDF版がダウンロードできます!笑
ここからは、「自分も技術書典に出してみようかな」と思う人に向けて、覚えておくと良いことを解説していきます。
執筆前
親方Project『技術同人誌を書こう!』をめっちゃ読みました。

技術同人誌を書こう! アウトプットのススメ (技術の泉シリーズ(NextPublishing))
- 作者: 親方Project
- 出版社/メーカー: インプレスR&D
- 発売日: 2018/04/13
- メディア: オンデマンド (ペーパーバック)
- この商品を含むブログ (1件) を見る
執筆から入稿、当日の準備まで網羅されていて、ほぼこれ一冊で同人誌が書けると思います。必携。
執筆環境
執筆環境にはRe:VIEWを採用しました。
Re:VIEW特有の記法を覚えなければいけませんが、同じ原稿から印刷用のPDFも、配布用のPDFも、電子書籍用のepubまで作成できるのはかなり魅力的です。 LaTeXやMarkdown、Wordといった手段を使うこともできましたが、どれもどこかに難を抱えていました。
RedPenやtextlintといった校正ツールは使いませんでした。イケてる執筆環境を整えている時間がなかったからです。 次回執筆するときは使うと思います。
エディタはVSCodeを使い、yet another Re:VIEW extensionを入れました。一番人気のextensionを使わずyet anotherを使っているのは、 一番人気のextensionがソースディレクトリ変更に対応していなかったからです。
Re:View記法は@<code>{hoge}のような特殊な記法になっていて、ベタ打ちするのはストレスフルです。
絶対にスニペットを登録しておきましょう。大幅な作業時間短縮になるはずです。
表紙作成
表紙は本文とは別ファイルで作る必要があります。アプリケーションとしてはAdobe Illustratorを使うのが間違いないと思います。
表紙の出来はそのまま売れ行きに直結しますので、可能であればデザイナーさんにお願いして作ってもらうのが良いでしょう。 僕は時間がなかったので自分でデザインしました……
かわいいライオンの画像はUnsplashからダウンロードしました。
本文が40ページを超えたくらいから背表紙をつけることを検討しましょう。本棚に並べたときの見栄えが段違いです。
入稿
日光企画に2日遅れで入稿しました。費用が10%UPでしたが、直接原稿を持ち込んで現金で決済したので5%OFFになりました。
入稿は直接持ち込むのが圧倒的におすすめです。その場で確認して、おかしいところがあったら指摘してくれます。 オンラインで入稿した場合、電話越しに修正ポイントを指摘され、改めてオンラインで入稿し、それに対してまた指摘があり、と何往復もする必要があります。 店員の方も「持ち込んでくれたほうが嬉しいですねー」と言っていたので、可能であれば御茶ノ水店に行きましょう。
原稿の受け渡しのため、USBメモリを持っていくとスムーズです。 ない場合、店舗にいながらオンラインで入稿する羽目になります。日光企画にはWiFiがないので、泣きながらテザリングしました。
印刷・製本方式はオンデマンドの平トジフルカラーにしました。 印刷方式はオフセットとオンデマンドの2種類が選べます。 オフセットのほうが写真などが綺麗に出ますが、オンデマンドのほうが安く、〆切も1日遅いです。技術書であればオンデマンドで良いと思います。 製本方式は平トジと中トジが選べます。平トジが普通の本です。ある程度ページ数があれば平トジ一択です。 本文はグレースケールで良いと判断したため、表紙のみをフルカラーにしました。
同人誌はなぜかB5サイズで作られることが多いですが、A5サイズにしたほうが(ページ数が増えたとしても)かなり割安です。特にこだわりが無ければA5サイズで作るのも良いと思います。
他にも遊び紙や表紙コーティングといった細かいオプションがたくさんあるのですが、実店舗に行けばサンプルが見られますし、丁寧に説明してもらえます。
前日準備・当日設営

長机の半分のサイズが各サークルに割り当てられます。スムーズに販売するためにはいろいろ必要なものがあるので、前日に慌ててハンズと100均(キャンドゥ)に駆け込みました。
①ブックカバー
キャンドゥとハンズの両方で買いましたが、100均のものはペラペラだったので捨てました。見本は心地よく読んでほしいですし、金額差も大したことは無いので良いものを選ぶべきだと思います。
②ブックスタンド
2つ必要だったので、キャンドゥとハンズの両方で買いました。一長一短。 迷ったら100均のもので良いと思います。
③布
布を敷くと見栄えがかなり良くなるので、絶対に買ったほうがいいです。
同人界隈ですと「あの布」が人気のようですが、僕は100均で端切れ布を買いました。十分でした。 たぶん何かしら敷かれていれば良いと思います。
④nu board
ホワイトボードやスケッチブックはその場で書き換えられるという点でなにかと便利です。
僕は結婚祝いで頂いたnu boardというノート型ホワイトボードをブックスタンドに立ててお品書きにしました。おすすめです。

Amazon限定 nu board (ヌーボード) B5判 NAB503BK08
- 出版社/メーカー: 欧文印刷
- 発売日: 2015/07/01
- メディア: オフィス用品
- この商品を含むブログを見る
他に買ったもの
- 名札
- 絶対あったほうがいいです。お客さんとのコミュニケーションが増えます
- ハードクリアファイル
- カード立て
- 今回は使いませんでしたが、頒布する書籍が複数ある場合、値札を立てておけるので便利だと思います
- メッシュポーチ
- お札の管理に使いました
あったらよかったもの
- 名刺
- 名刺をいくつかいただきましたが、プライベート用の名刺を作っていなかったのでお返しできませんでした……
その他こまごまとしたTips
執筆・印刷
- ダウンロードカードは用意する
- 準備が面倒なので今回はやらなかった
- かんたん後払い利用者のみ、公式の機能としてダウンロード機能があるのでそれを使った
- 「ダウンロードカードもらってません」という問い合わせが頻発した
- 気持ち多めに刷る
- 余ったからと言って即座に赤字なわけではない
- ダイレクト入庫というサービスを使うことで、とらのあなやBOOTHに簡単に委託することができる
- 手元にある程度残しておけば「ほしい」と言われたときに渡すことができる
- なにより、「もう本ないんですか……」という悲しい顔を見ずに済む
- お問い合わせ用の連絡先や、ツイートするときのハッシュタグを本文に書いておく
- ないと反応が全然見えなくてつらい
- 間違いの指摘も来ないので、次版の修正ができない可能性がある
準備
- サークルカットは早めに作っておく
- 一般の人がサークルリストにアクセスできるまでに作っておくと被チェックの伸びが良いと思う
- 書き終えたら宣伝が命
- ちょっとしつこいぐらいツイートした。特に前日〜当日にかけて。その甲斐あって被チェック数はぐぐっと伸びたし、BOOTH版も伸びた
- 公式の推し祭り(Twitterイベント)には必ず参加する
- かなり被チェックが伸びる
- 他の出展者の方からフォローされ、交流が始まることも
- 値段設定は1000円にしておくとめっちゃ楽
- 書籍とPDFのセットは1500円に設定して、支払い方法をかんたん後払いのみにした
当日
- 交代要員は絶対用意する
- ワンオペだとトイレ行くだけで詰みかねないし、自分の買い物もできない
- 隣のブースだったカレーちゃん(@currypurin)がワンオペで捌いていてマジですごいと思った
終了後
- 出納をつける
- いくら使って、いくら入ったのか把握して次回の部数設定に活かす
- 翌日以降もPDF版などを宣伝する
- 技術書典行けなかったけど評判いい本があったら買いたいという人はたくさんいる
- ちゃんと宣伝すると、技術書典と同じくらい売れる
- 振り返りブログを書く
- 思いついた反省点をさっぱり忘れてしまうともったいない
最後は時系列で技術書典を振り返っていきます。
ツイートで振り返る経緯
機械学習のアンチパターン集ってあんまりないな、と思ってツイートしてみたら、なんとなくいい反応だったので軽い気持ちで書いてみようかと思う。 何なら技術書典をtypoするという体たらく。
機械学習(Kaggle)やっちゃだめだよパターン集とか、技術書店に出したら売れそう(やるか?)
— えじ|Amane Suzuki (@SakuEji) 2019年6月30日
ただ、実はその日、技術書典の〆切当日。
技術書典、サークル申し込みあと30分くらいじゃんwwww
— えじ|Amane Suzuki (@SakuEji) 2019年6月30日
フォームを必死に記入しながら、技術書典経験者のu++さんとカレーちゃんに聞いてみる。 大丈夫だよーみたいな反応を貰ったので必死に申し込み作業を行う。
@upura0 @currypurin 技術書典って準備期間どれくらいかかるものですか? 予めある程度原稿ないときついでしょうか?
— えじ|Amane Suzuki (@SakuEji) 2019年6月30日
いま必死にフォーム記入してます笑
— えじ|Amane Suzuki (@SakuEji) 2019年6月30日
ギリギリ申し込み終了。
技術書展に「天色グラフィティ」で申し込みしましたー! #技術書典https://t.co/1grBZSkhlg
— えじ|Amane Suzuki (@SakuEji) 2019年6月30日
なんと当選。この日のうちにRe:VIEWの執筆環境を整える。後から考えると、ここで環境をきちんと作っていなかったら本は出てなかった。
ちなみに、本当にほとんど何も進んでいない。
技術書典7通ってました!! まだほとんど何も進んでないけど頑張ります!! #技術書典 pic.twitter.com/7EugXqjnBP
— えじ|Amane Suzuki (@SakuEji) 2019年7月10日
Kaggle Meetupに参加した時、『Kaggleのチュートリアル』を執筆したカレーちゃんと会う。「書いてます?」という問いに対し、苦笑いで返す。 「えじさんの本売れると思いますし、たくさん刷ったほうがいいですよ! 600部とか!」と言われ、「この人、俺を殺しに来てるんじゃないか」と思った記憶がある。
カレーちゃんさんに技術書典での部数をどれくらいにしたらいいか聞いたら「いいからどんどん刷ろう(意訳)」な感じだったので沢山刷ることを前向きに検討し始めた
— えじ|Amane Suzuki (@SakuEji) 2019年7月13日
エルピクセルさんの勉強会に行ったり、もくもく会を主催したり、KDD行ったり、他の記事を執筆したりでしばらく原稿の進捗がない日々が続く。
シアトルのamazon goに来た。「これマジでちゃんと会計されんの!?」とかみんなで大騒ぎしながら買い物して、初めてコンビニ来た人の気持ちを理解した気がする pic.twitter.com/PWGjYE0bRq
— えじ|Amane Suzuki (@SakuEji) 2019年8月10日
同じ部署の一樹さん(@ikki407)山川さん(@yiemon773)と書いた記事が出ました〜データを眺めるところから評価指標の決定、モデル作成、パラメータチューニングまで、基礎的なところを広くさらった内容になってます。かなりのボリュームだと思います。ぜひ読んでみてください!https://t.co/yhhZK833nt
— えじ|Amane Suzuki (@SakuEji) 2019年9月10日
カレーちゃんのブースが隣だということが分かる。カレーちゃんは超人気サークル主。しかもジャンルが近いので、一緒に買っていってくれる人が多いに違いない。勝利を確信する。ちなみにこの時点で進捗は3割くらい。
技術書典、カレーちゃん隣マジか! 心強い……ちなみに本は鋭意進捗中です……
— えじ|Amane Suzuki (@SakuEji) 2019年9月10日
「完成しさえすれば勝ち」と自分に言い聞かせながら必死に原稿を書く。Twitterへの浮上が減る。もちろんTwitterをしていないのでモリモリ原稿ができていく。
そして完成。
『ハマって覚えるデータ分析・機械学習の罠』を頒布します!
— えじ|Amane Suzuki (@SakuEji) 2019年9月21日
小規模な機械学習プロジェクト(研究やKaggleを含む)でやらかしがちなことを広く紹介します。機械学習初心者〜中級者向けです。
技術書典7【く15D】で僕と握手!
(PDF版も同時頒布予定ですので、来れない人はそちらをどうぞ)#技術書典 pic.twitter.com/wnv26dOXYY
以後は技術書典当日。
開始前にBOOTHで10人以上に購入いただき、びっくりする。
『ハマって覚えるデータ分析・機械学習の罠』BOOTH版、すでに10人以上の方にご購入頂いています……!https://t.co/lTDvHFu2zQ#技術書典 来られるという方はこちらからチェック! 【く15D】にてお待ちしています!https://t.co/Drs4TEU9md pic.twitter.com/aOuSPIkhJ8
— えじ|Amane Suzuki (@SakuEji) 2019年9月22日
12:00ごろ、開始1時間で半分売り切れてビビる。
#技術書典 【く15D】で頒布中の『ハマって覚えるデータ分析・機械学習の罠』ですが、開始1時間の時点でたくさんの方にご購入いただき、書籍版が半分ほど売れました。
— えじ|Amane Suzuki (@SakuEji) 2019年9月22日
書籍が売り切れますとPDF版のみの販売となりますので、書籍がほしい!という方はお急ぎください!
(次回はもっとたくさん刷ります><)
13:00ごろ、早々に完売が見えてくる。
#技術書典 【く15D】で頒布中の『ハマって覚えるデータ分析・機械学習の罠』ですが、予想を上回る売れ行きにより、書籍の残りがこれだけとなっています><
— えじ|Amane Suzuki (@SakuEji) 2019年9月22日
完売の場合はPDFのみの販売となります pic.twitter.com/5CnSy8isvl
無事14:00ごろに売り切れ、PDF版をゆるゆる頒布。
#技術書典
— えじ|Amane Suzuki (@SakuEji) 2019年9月22日
無事150部完売しました〜〜☺️☺️☺️
買いに来てくださった方、BOOTHで買ってくださった方、ほんとうにありがとうございました!! 物理本早々に売り切れてすいません!!
めっちゃ楽しかった!!!!
かなり身軽にブース運営していたので、5分で撤収完了。カレーちゃんに「撤収速いですね!」と言われてドヤ顔で撤収するも、駅までの道で迷う。
終了後5分で颯爽撤収したのに駅に行くまでで迷った
— えじ|Amane Suzuki (@SakuEji) 2019年9月22日
たくさん買い物した。
#技術書典 戦利品です!ほかにもダウンロードカードがいくつか。頑張って読みます〜 pic.twitter.com/ORNgTKFK4W
— えじ|Amane Suzuki (@SakuEji) 2019年9月22日
翌日以降もたくさん買っていただいています!
BOOTH版も続々と買っていただき、書籍PDF合計で300部ほど売れています! 技術書典すごい……https://t.co/lTDvHFu2zQ
— えじ|Amane Suzuki (@SakuEji) 2019年9月23日
まとめ
完成が危ぶまれた時期もありましたが、それを含めてすべて楽しかったです!また次回も(新刊をつくって)参加したいと思います!
技術書典8で会いましょう!
自作キーボード沼への第一歩。Lily58を組み立てました!
みなさんは遊舎工房をご存知でしょうか?
遊舎工房とは、秋葉原(御徒町)にある自作キーボードの専門店です。 おそらく日本唯一の専門店で、かつ店内に工作スペースがあり、購入したキーボードを組み立てて帰ることができます。
開店当初から行きたいと思っていたのですが、なかなかきっかけが掴めずにいました。 しかし、社内でセパレートキーボードを使っている同期をみているうちにキーボード欲が刺激されてしまいました。
Lily58を作っている様子
今回購入したのはLily58という、自作キーボード界隈でも人気のセパレートキーボードキットです。

Lily58には基盤や電子部品はすべて含まれていますが、キースイッチ(入力を感知するスイッチ部分)とキートップ(実際に指が当たる部分。印字されてたりする)は別に購入する必要があります。
箱の左に置いてあるのがキースイッチです。キースイッチには 癖のない赤軸、スイスイ打てる茶軸、めっちゃ軽い白軸、重みのある黒軸、カチカチ音がなる青軸といろいろあり、おそらく沼ポイントのひとつです。
僕は赤軸で、静音性を重視したものを選びました。HHKBのスコスコ音も嫌いではないですが、やはり静かな空間に行くと浮いてしまいます(セパレートなんて持っていったらもっと浮くというツッコミは無しでお願いします)

高校以来のはんだ付けでした。中高6年間やっただけあって、腕は鈍っていなかったよう。ミスひとつなく作れました。
Lily58ははんだ付けをするポイントが結構多いので、はじめての人は店員の方にサポートしてもらいながら作ると良いと思います。

はんだ付けをする妻です。「えっえっ大丈夫かなねえこれ本当に大丈夫?」と大騒ぎしていましたが、終わってみれば彼女の担当した場所もノーミスでした。すごい。

今回購入したのは正確にはLily Proというもので、キースイッチを後から付け替えることができるタイプになっています。
要するに、キースイッチ沼にはまりやすい代物ということですね。

キートップは白の無刻印を選びました。
Lily58を始めとする自作キーボード群には、レイヤーという機能が存在します。これは、一部のキーを押すと配列がガラッと切り替わって、記号やファンクションキーなどをホームポジション付近で押せるようになるというものです。
要するに、初期のキー配置なんて、書いてあっても書いてなくても一緒なのです(と僕は解釈しました)
まとめ
作業時間の内訳は、
- キットを選ぶ(30分)
- はんだ付け(2時間)
- 動作確認(30分)
- キートップをはめる(45分)
- 眺めてうっとりする(15分)
で総計4時間といったところでしょうか。はんだ付けに慣れていない場合は+2時間くらいを見積もっておくと良いかもしれません。
使ったお金は、
- Lily58 Pro MX 15984円
- Gateron Silent スイッチ 赤軸 75円×58個 = 4350円
- TRRSケーブル(左右をつなぐやつ) 324円
- USBケーブル 540円
- キートップセット 2640円
で、合計23838円です。だいたいキットの値段+8000円くらいと思っておくと良いでしょう。
肝心の使ってみての感想ですが、
- 最初は慣れない。特にエンターとバックスペースを親指で取るのが耐えられない
- column staggered(列ごとに揃っている)配列なので、CVBNMあたりをめちゃめちゃミスタイプする
といった感じのつらみがあります。最初は。1日実戦投入したらだんだん慣れてきたので、1週間くらいしたら使いこなせると思います。
一方、さっきMac備え付けのキーボードを短時間触ったら、すげー変な感触とともに大量のミスタイプが発生しました。共存はだいぶ厳しいかもしれません。
一度入ってしまったら戻れない。沼たる所以はこんなところにもあったのです。
セパレートにしたいけど、普段のキーボードも使わなきゃいけない事情がある。そんな人にはMint60という素晴らしいキーボードがあるようです。 遊舎工房の通販サイトにはありませんが、実店舗では売っていました。
みなさんも、楽しい自作キーボードの世界に飛び込んでみませんか?





![LeanとDevOpsの科学[Accelerate] テクノロジーの戦略的活用が組織変革を加速する impress top gearシリーズ LeanとDevOpsの科学[Accelerate] テクノロジーの戦略的活用が組織変革を加速する impress top gearシリーズ](https://m.media-amazon.com/images/I/51TuqLnPBCL._SL500_.jpg)









